Auf dieser Seite kannst Du Dir ganz in Ruhe alleine etwas beibringen, ohne, dass Dich Dein Lehrer oder sonst wer nervt. Gerne kannst Du auch Deinen Lehrer fragen, wenn Du etwas nicht verstehst. Arbeite alles von vorne nach hinten durch. Allerdings ist es wichtig, dass Du Dir wirklich etwas beibringst. Du kannst zwischendurch immer wieder testen, ob Du alles verstanden hast. So bist Du auch fit für den Test, der am Ende kommen wird.
Ok, es geht los!
1.Mechanik -was ist das eigentlich?
Vielleicht hast Du das Wort „Mechanik“ schon mal gehört. Oder das Wort „Automechaniker“. Aber was heißt das eigentlich? Das zu erklären ist gar nicht so einfach. Es geht eigentlich immer um Bewegung. Warum sich etwas bewegt, warum nicht oder wie es sich bewegt. So kümmert sich ein Automechaniker vor allem darum, dass sich ein Auto (wieder) bewegt, wenn es kaputt ist.
In der Physik geht es bei dem Thema aber um noch viel mehr!
Eine wichtige Frage ist zum Beispiel, warum sich etwas bewegt? Was meinst Du, warum bewegt sich etwas?
OK, Du solltest jetzt schon etwas ganz Wichtiges gelernt haben. Vervollständige den folgenden Satz. Wenn er richtig angezeigt wird, dann sollst Du den Satz in Deinen Physikhefter übertragen. Überschrift: Mechanik – Kräfte. Danach Merksatz 1: (dort schreibst Du dann den folgenden Merksatz ab)
Wenn eine Kraft auf einen Körper einwirkt gibt es zwei Möglichkeiten: 1. der Körper wird schneller. Man spricht dann von einer Beschleunigung. Oder 2. Der Körper wird langsamer. Dann spricht man von einer Verzögerung. Aber Kräfte können noch mehr! Sie können außerdem etwas Verformen oder dafür sorgen, dass ein Körper seine Richtung ändert.
Finde so schnell wie möglich die Paare!
Ok, noch einmal. Fülle die Lückentexte aus!
Übertrage den Merksatz Nr. 2 in Deinen Hefter oder Heft:
Kräfte können von einem Körper die Geschwindigkeit oder die Bewegungsrichtung verändern. Auch können Sie ihn verformen.
Für Kräfte benutzt man das Formelzeichen F . Die Kraft misst man in der Einheit Newton (1N).
Kräfte kann man nicht sehen. Man kann nur sehen, was sie bewirkt haben. Aber man kann Kräfte messen. Z.B. mit einem Kraftmesser. Sie bestehen aus einer Feder, die durch die Kraft verformt wird.
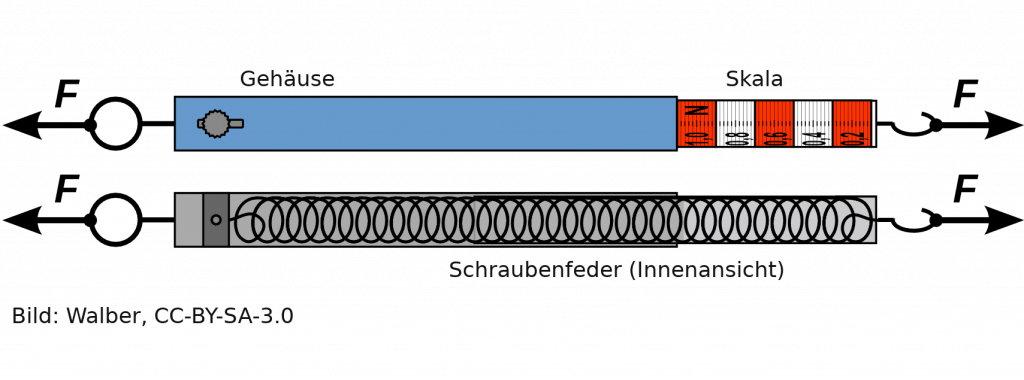
Will man auf einer Zeichnung Kräfte darstellen oder sichtbar machen, so benutzt man dafür einen Pfeil. Ein Pfeil zeigt, in welche Richtung die Kraft wirkt. Seine Länge gibt die Stärke der Kraft wieder.
Kräfte werden durch Pfeile dargestellt
Eine Kraft wird als Pfeil gezeichnet. Dieser Pfeil ist dann ein sogenannter Vektor.
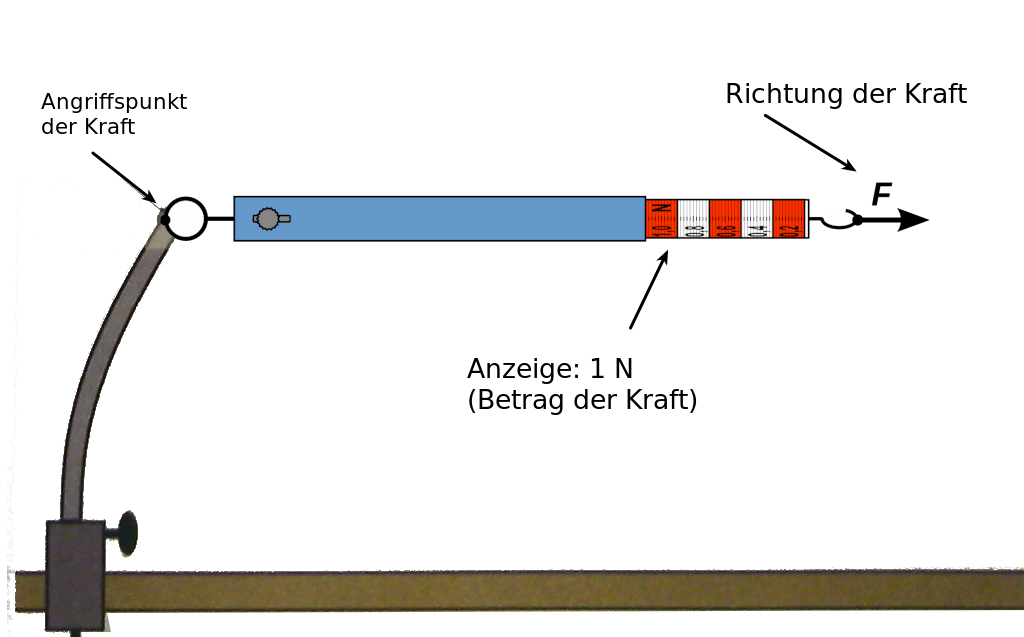
Pfeilanfang: Angriffspunkt der Kraft
Pfeilspitze: Richtung der Kraft
Pfeillänge : Größe der Kraft
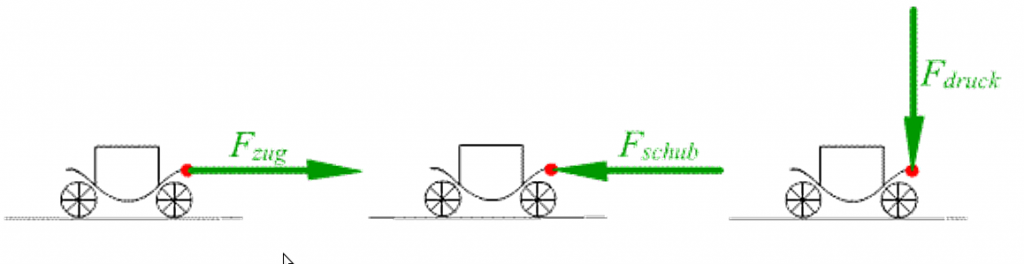
Gehen zwei Kräfte in die gleiche Richtung, so können sie addiert werden.
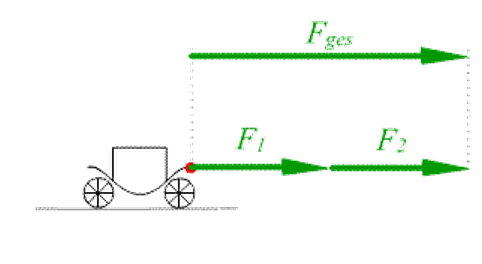
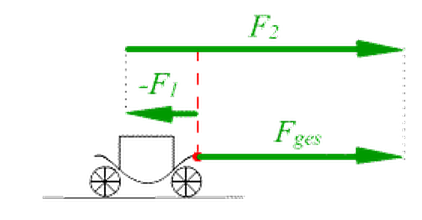
Die Kutsche wird von den zwei Pferden gezogen (F2), und bekommt Gegenwind (-F1). Die Gesamtkraft ergibt sich aus
F1-F2.
Zusammensetzung von Kräften
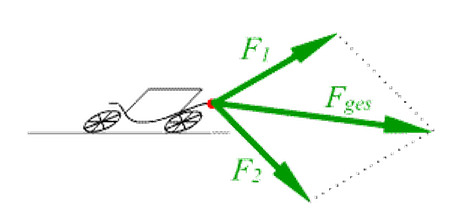
Verschieden gerichtete Kräfte:
Wenn die zwei Pferde nicht in dieselbe Richtung laufen, muss zeichnerisch wie folgt addiert werden. Dabei entsteht das sogenannte „Kräfte-Parallelogramm“: FR ist dabei die resultierende Kraft. Wenn Du nicht weißt, was“resultierend“ bedeutet, benutze die Hilfe, um es Dir selbst zu erklären.
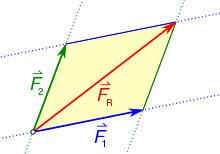
So kannst Du per Zeichnung die resultierende Kraft bestimmen:
Stell dir vor, du hast zwei Kräfte, die auf einen Gegenstand wirken. Diese Kräfte sind wie unsichtbare Pfeile, die den Gegenstand schieben wollen.
Um herauszufinden, wo der Gegenstand hingeht, musst du ein spezielles Muster zeichnen. Denk an ein Rechteck ohne rechte Winkel, das heißt, die Seiten sind schräg.
Jetzt zeichnest du die Kräfte als Pfeile innerhalb dieses Rechtecks. Die Länge der Pfeile zeigt an, wie stark die Kräfte sind.
Wenn du die Enden der Pfeile miteinander verbindest, entsteht eine schräge Linie.
Die resultierende Kraft ist die, die vom Anfang des Rechtecks zur Spitze dieser schrägen Linie zeigt. Das zeigt dir, in welche Richtung die Kräfte den Gegenstand ziehen.
Noch einfacher ausgedrückt: Stell dir vor, du hast zwei Hunde an einer Leine. Sie ziehen in verschiedene Richtungen. Das Rechteck zeigt dir, wohin sie dich ziehen würden, wenn du sie genau in die Mitte des Rechtecks bringst und nach vorne schaust. Zu kompliziert? Dann suche dir ein Video, dass es dir erklärt. Z.B. das hier: https://www.youtube.com/watch?v=JdihgTx_kW8
Aufgabe:
Folgende Aufgabe solltest Du jetzt alleine lösen können:
Ein Kind geht mit zwei Hunden spazieren. Zwischen den beiden Leinen besteht ein Winkel von 90 Grad. Die Hunde ziehen mit 90 und 60 N. Ermittle die resultierende Kraft. Benutze die Hilfe, wenn Du nicht weiter kommst. Das Ziel ist aber es alleine zu können.
Test
Du solltest jetzt in der Lage sein, Kräfte zu addieren und zu subtrahieren. Und Du solltest bei zwei Kräften in unterschiedlicher Richtung in der Lage sein, die resultierende Kraft zu bestimmen bzw. auszurechnen.
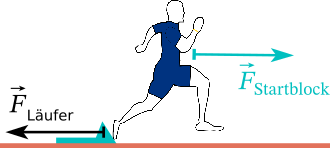
Kraft und Gegenkraft
Wenn du einen Fußball trittst, übst du eine Kraft auf den Ball aus. Die Kraft kann den Ball dazu bringen, sich zu bewegen oder seine Geschwindigkeit zu ändern. Das ist jetzt für Dich nichts Neues mehr.
Aber hier kommt die verrückte Sache mit der Gegenkraft ins Spiel. Gegenkraft ist die Reaktion auf die ursprüngliche Kraft. Das bedeutet, dass das Objekt, auf das die Kraft ausgeübt wird, eine gleich große Kraft in die entgegengesetzte Richtung ausübt. Aufgabe: überprüfe mit einem Lineal, ob in der folgenden Zeichnung die beiden Kraftpfeile wirklich genau gleich sind, oder ob vielleicht ein Fehler unterlaufen ist.
Lass mich das anhand eines Beispiels erklären. Stell dir vor, du stehst auf einem Skateboard und schiebst deinen Freund oder Deine Freundin weg. Wenn du sie oder ihn nach hinten schiebst, übst du eine Kraft auf ihn aus. Gleichzeitig übt dein Freund eine Gegenkraft auf dich aus, indem er dich nach vorne schiebt.
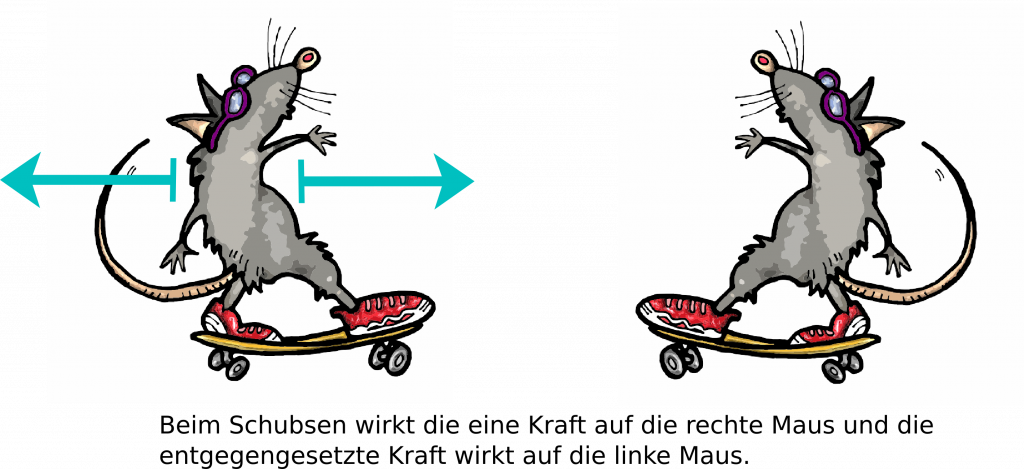
Das ist das Prinzip von Kraft und Gegenkraft. Jede Aktion erzeugt eine Reaktion, oder anders gesagt, jede Kraft hat eine gleich große Gegenkraft. Das nennt man auch das dritte Newtonsche Gesetz der Bewegung, benannt nach Sir Isaac Newton.
Masse und Gewichtskraft
Die Masse gibt an, wie leicht oder schwer etwas ist. In einer Formel wird die Masse mit einem „m“ abgekürzt. Die Einheit der Masse kennst Du bestimmt schon. Die Masse wird in der Einheit Kilogramm (1kg) oder Gramm (1g) gemessen. Die Masse von einem Körper ist immer gleich, egal wo man ist. Also z.B. mMensch = 62 kg.

Aber jetzt kommt’s : In der Physik unterscheidet man zwischen Masse und Gewicht. Die Masse ist überall gleich. Das Gewicht nicht!!!
Und das hängt mit der Gewichtskraft zusammen.
Die Gewichtskraft ist die Kraft, die auf einen Gegenstand wirkt, wenn er sich in der Nähe der Erde befindet. Sie wird verursacht durch die Anziehungskraft der Erde auf den Gegenstand. Je größer der Gegenstand ist, desto stärker ist die Gewichtskraft. Verstehst du das bis hierhin?
Die Gewichtskraft zeigt immer nach unten, zur Erde hin. Das liegt an der Anziehungskraft der Erde. Sie sorgt dafür, dass wir auf dem Boden bleiben und nicht im Weltraum herumfliegen. Wenn Du Springen spielst, dann wirkt die Gewichtskraft auch, wenn Du wieder auf den Boden kommst und Dich wieder hinsetzt.
Aufgabe: Fertige in Deinem Heft eine Zeichnung an, die das wieder gibt, was Du gerade über die Gewichtskraft gelesen hast.
Um die Gewichtskraft zu messen, benutzt man eine Feder-Waage. Die Feder-Waage zeigt Dir, wie stark die Gewichtskraft Deines Körpers ist. Wie viel Du wiegst, hängt von Deiner Masse ab. Je mehr Masse Du hast, desto größer ist Deine Gewichtskraft.
Der Ortsfaktor
Aber es hängt auch davon ab, wo Du Dich gerade befindest. Auf dem Mond wird Deine Masse weniger stark angezogen als auf der Erde. Auf dem Mars wird man ebenfalls weniger stark angezogen. Aber auch auf der Erde macht es einen Unterschied, ob man am Äquator oder in der Nähe des Nordpols steht. Man spricht deshalb vom Ortsfaktor. Wenn man ein Gewicht ganz genau angeben will, so muss man den Ortsfaktor mit angeben.
Die Gewichtskraft (FG berechnet man so: FG = m * g Wobei g der Ortsfaktor ist.
Auf der Erde ist der Ortsfaktor im Durchschnitt 9,81 (gerundet 10). Am Nordpol ist er niedriger als auf dem Mount Everest. Auf dem Mond ist er 1,62. Und auf der Sonne 274.
Formeln umstellen
Manchmal ist es wichtig eine Formel so umzustellen, dass sich ein Buchstabe der Formel alleine auf einer Seite des Gleichheitszeichens befindet. Man sagt: Die Formel muss aufgelöst werden. Z.B. kann man die Formel FG = g * m nach g auflösen. Anschließend kann man die Werte, die man z.B. für FG und m hat einsetzen und g ausrechnen. Wie das genau geht ist hier Schritt für Schritt erklärt. Diese Arbeitsweise musst Du können. Übe es so lange, bis Du es ohne Hilfe kannst:
Vertausche die beiden Seiten der Gleichung.
\[\color{Red}{{g}} \cdot {{m}} = {{F_{\rm{G}}}}\]
\[\frac{\color{Red}{{g}} \cdot {{m}}}{{{m}}} = \frac{{{F_{\rm{G}}}}}{{{m}}}\]
Vertausche die beiden Seiten der Gleichung.
\[{{g}} \cdot \color{Red}{{m}} = {{F_{\rm{G}}}}\]
\[\frac{{{g}} \cdot \color{Red}{{m}}}{{{g}}} = \frac{{{F_{\rm{G}}}}}{{{g}}}\]
Und noch eine leichte Übung:
Aufgabe: Beschreibe in Deinem Heft oder Hefter unter einer passenden Überschrift den Unterschied zwischen Masse und Gewichtskraft.
Die Ursache der Gewichtskraft
Die physikalische Ursache für die Gewichtskraft ist die Massenanziehung, auch Gravitation genannt. D.h. zwei Massen ziehen sich gegenseitig an. Also Die Erde (Masse 1) zieht einen Menschen (Masse 2) an. Aber gleichzeitig zieht der Mensch auch die Erde an. Nur wesentlich weniger stark. Die Größe der Gravitationskraft wird vom Abstand der sich anziehenden Körper und ihren Massen beeinflusst.

Hookesches Gesetz
Das Hooke’sche Gesetz ist eine Regel, die besagt, dass die Ausdehnung oder Verkürzung eines elastischen Materials proportional zur ausgeübten Kraft ist. Was bedeutet das? Nun, stell Dir vor, Du hast ein Gummi- oder Federband in der Hand. Wenn Du es dehnst oder zusammendrückst, übst Du eine Kraft auf das Material aus, richtig? Das Hooke’sche Gesetz sagt uns, dass die Veränderung der Länge des Materials direkt proportional zur ausgeübten Kraft ist. Wir nehmen als Material jetzt einfach mal eine Feder aus Stahl.
Kraftwirkung auf elastische Körper

Das Gesetz von HOOKE beschreibt die Wirkung einer Kraft auf elastische Körper. Dies sind z.B. Federn oder Gummibänder. Federn gehen in ihre ursprüngliche Lage zurück.
Auf die links aufgehängte Feder in Abb. 1 wirkt nur ihre Gewichtskraft FG, da an sie keine Kugel angehängt ist. Sie hat die Länge x0. Belastest Du die Feder z.B. durch Anhängen einer Kugel, so wirkt zusätzlich eine Kraft FKugel auf die Feder. Insgesamt wirkt jetzt also die Kraft F= F0.+ FKugel auf die Feder. (F0 ist die Kraft, die auf die Feder ohne Kugel wirkt.)
Die Feder dehnt sich aus und hat nun mit angehängter Kugel die Länge x. Die Längenänderung Δx der Feder ist also Δx= x- x0 . Das liest sich erst einmal alles sehr kompliziert. Aber lese noch einmal Satz für Satz und vergleiche ihn mit der Abbildung. Dann wird es verständlich.
Natürlich hängt die Längenänderung auch von der Masse der Kugel ab. Also von der jeweiligen Gewichtskraft. ABER: Je größer die Kraft, desto länger dehnt sich auch die Feder aus. Die Ausdehnung hängt aber von der jeweiligen Feder ab. Eine aus dünnem Stahl dehnt sich stärker aus, als eine aus dickem. Man spricht deshalb von einer Federkonstante D .
D = Kraftänderung : Längenänderung
Beobachte, was sich verändert, wenn Du eine Kraft einstellst und anschließend die Federkonstante veränderst. Schreibe anschließend unter der Überschrift „Zusammenhang zwischen Federkonstante und wirkende Kraft“ mindestens drei Sätze, die den Zusammenhang erklären.
Aufgabe: Miss die Verlängerung einer Feder bei verschiedenen Massestücken aus. Lege eine Messtabelle in Deinem Hefter an und zeichne ein Diagramm. Überschrift: Die Federkonstante D
Reibungskräfte
Die Haftreibung spielt im täglichen Leben eine wichtige Rolle. Hier sind drei Beispiele:
1. Radfahren auf nasser Straße: Beim Radfahren auf nasser oder rutschiger Straße spielt die Haftreibung zwischen den Reifen und der Fahrbahnoberfläche eine entscheidende Rolle. Die Haftreibungskraft ermöglicht es den Reifen, ausreichend Grip auf der Straße zu haben, um das Fahrzeug zu kontrollieren und ein Abrutschen oder Ausbrechen zu verhindern.

2. Öffnen von Schranktüren: In einem Haushalt hat man oft Schranktüren, die geöffnet und geschlossen werden müssen. Die Haftreibung zwischen den Türscharnieren und der Struktur des Schrankes sorgt dafür, dass die Türen in Position bleiben und nicht ungewollt auf- oder zuschnappen.
3. Bewegen von Möbeln: Beim Bewegen von Möbeln in einem Raum spielt die Haftreibung eine Rolle zwischen den Möbelbeinen und dem Boden. Die Haftreibungskraft verhindert ein ungewolltes Verschieben der Möbelstücke und ermöglicht es, die Möbel kontrolliert und sicher zu bewegen.
Darstellung der Kräfte beim Anschieben einer Kiste, die zunächst auf dem Boden haftet. Hat sich die Kiste einmal in Bewegung gesetzt, braucht es nur noch eine geringere Kraft, um die Bewegung beizubehalten.

Abbildung Reibungskräfte: Debenben – Eigenes Werk, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=31801913
<iframe src=“https://phet.colorado.edu/sims/html/friction/latest/friction_de.html“ width=“800″ height=“600″ allowfullscreen></iframe>
Aufgabe: Übertrage die richtigen Sätze in Deinen Hefter oder ins Heft. Überschrift: Haftreibung
Übrigens entsteht bei der Reibung auch immer Wärme (energie). Das veranschaulicht sehr schön diese Simulation:
Wenn Du das Thema vertiefen möchtest: https://www.leifiphysik.de/mechanik/reibung-und-fortbewegung/grundwissen/haft-gleit-und-rollreibung
Haftreibungskoeffizient
Je nachdem welche Materialien aufeinander reiben gibt es einen „ Haftreibungskoeffizient“. Wenn ich diesen „Haftreibungskoeffizienten“ kenn, kann ich ausrechnen, wie viel Kraft ich brauche, um etwas zu bewegen.
Haftreibungskraft = Haftreibungskoeffizient * Normalkraft
Der folgende Rechner hilft Dir Haftreibungskraft, Haftreibungskoeffizient und Normalkraft auszurechnen.
Haftreibungssimulation
Löse damit jetzt die folgenden zwei Textaufgaben. Achtung, es ist nicht einfach diese Aufgaben zu lösen. Benutze die Hilfe, um die Aufgaben zu lösen und es Dir erklären zu lassen.
Übertrage die folgenden Aufgaben in Deinen Hefter oder ins Heft. Überschrift: Haftreibung – Übungen
Übungsaufgabe 1:
Lisa möchte einen schweren Schrank über den Boden in ihrem Zimmer verschieben. Der Schrank wiegt 100 kg. Lisa übt eine Kraft von 150 N in horizontaler Richtung aus, um den Schrank zu bewegen. Der Haftreibungskoeffizient zwischen dem Schrank und dem Boden beträgt 0,4. Berechne die Haftreibungskraft und überprüfe, ob Lisa den Schrank bewegen kann.
Lösung:
Antwortsatz:
Übungsaufgabe 2:
Sophie möchte einen schweren Einkaufswagen in einem Supermarkt bewegen. Der Einkaufswagen hat eine Masse von 25 kg. Sophie übt eine horizontale Kraft von 50 N aus, aber der Einkaufswagen bleibt stehen. Der Haftreibungskoeffizient zwischen dem Einkaufswagen und dem Boden beträgt 0,6. Berechne die maximale Haftreibungskraft zwischen dem Einkaufswagen und dem Boden.
Hinweis: Um die Haftreibungskoeffizienten bzw. die maximale Haftreibungskraft zu berechnen, verwende die entsprechende Formel für die Haftreibungskraft und setze die gegebenen Werte ein. Denke daran, dass die Haftreibungskraft die angewandte Kraft ausgleicht und die Bewegung verhindert, solange sie nicht den Wert der maximalen Haftreibungskraft übersteigt.
Physikalische Arbeit
Du kennst das Wort „Arbeit“ natürlich schon. Aber was bedeutet es eigentlich ganz genau?
Im Alltag bedeutet Arbeit, dass man etwas macht. In der Physik sind wir etwas genauer!
Ein Beispiel:
Physikalische Arbeit ist, wenn du einen schweren Koffer eine Treppe hinaufschleppst. Du brauchst Kraft, um den Koffer zu bewegen. Und du bewegst ihn auch eine Strecke hoch.
Aber denk daran, nicht alles, was du anpackst, ist Arbeit im physikalischen Sinn. Wenn du einfach nur den Koffer festhältst und stillstehst, machst du keine Arbeit. Die Arbeit passiert nur, wenn du Kraft anwendest und gleichzeitig eine Strecke zurücklegst.
Also: Arbeit = Kraft mal Weg
Als Formel: W = F*s (W ist das Formelzeichen der Arbeit -vom Englischen Wort „Work“ , s =Strecke und F = Kraft)
Natürlich hat die Arbeit auch eine Einheit:
Die Einheit der Kraft ist Newton (N). Die Einheit der Strecke ist das Meter (m). Also ist die einheit der Arbeit das Newtonmeter (Nm). Neuerdings wird aber auch die Einheit Joule (J) verwendet.
1 Newtonmeter = 1 Joule
1 Nm=1J
1000J=1kJ
Aufgabe schreibe in Deinem Hefter oder Heft auf, was physikalische Arbeit ist.
Hubarbeit
Wenn etwas hochgehoben wird, spricht man von Hubarbeit.
Hubarbeit = Hubkraft mal Höhe
Als Formel: W= FG*h
Aufgabe1: Schreibe in Deinen Hefter oder Heft jeweils drei Beispiele für Arbeit und drei Beispiele für Hubarbeit. Überschrift: Arbeit und Hubarbeit
Aufgabe 2: Hubarbeit
Stell dir vor, du hebst einen Koffer mit einer Masse von 10 Kilogramm vom Boden auf einen Tisch, der 1 Meter hoch ist. Wie viel Hubarbeit verrichtest du, um den Koffer auf den Tisch zu heben?
Lösungstipps:
- Masse des Koffers (m) =
- Höhe des Tisches (h) =
- Erdbeschleunigung (g) ≈ 9,8 m/s²
- Formel für die Hubarbeit:
- Erinnere Dich: wir haben gesagt, dass die Kraft um etwas hochzuheben wie folgt berechnet wird: F=m*g
- Manchmal ist es auch hilfreich sich eine Skizze auf einem Schmierblatt zu machen.
Masse des Koffers (m) = 10 kg
Höhe des Tisches (h) = 1 m
Erdbeschleunigung (g) ≈ 9,8 m/s²
Die Hubarbeit (W) wird mit dieser Formel berechnet: W = m * g * h
W = 10 kg * 9,8 m/s² * 1 m = 98 Joule
Antwort: Du verrichtest 98 Joule Hubarbeit, um den Koffer auf den Tisch zu heben.
Übe diese Aufgabe so lange, bis Du sie verstanden hast und alleine lösen kannst.
Die Leistung
Von Leistung spricht man, wenn Arbeit in einer bestimmten Zeit erledigt wird. Klar, wenn Klara die Getränkekiste in zwei Minuten die Treppe hoch schleppt, dann hat sie mehr geleistet, als wenn Max dafür 20 Minuten braucht.
Leistung ist also Arbeit (W) geteilt durch die dafür benötigte Zeit (t)
Das Formelzeichen für die Leistung ist P
Also kommen wir auf die Formel:
P= W/t
Die Einheit der Leistung ist das Watt (W)
1J/1s=1W Also ein Watt ist, wenn die Arbeit von einem Joule in einer Sekunde verrichtet wird.
Aufgabe: Beschreibe mit Deinen eigenen Worten, was Leistung bedeutet.
Denke dir dazu auch eine schöne Aufgabe aus.
Danach löst Du die folgende Aufgabe in Deinem Hefter oder Heft.
Überschrift: Die Leistung
Stell dir vor, du hebst einen Koffer mit einer Masse von 20 Kilogramm in einer Zeit von 10 Sekunden auf eine Höhe von 2 Metern. Berechne die mechanische Leistung, die du bei diesem Vorgang erbringst.
Gehe wie folgt vor:
gegeben (geg.):
gesucht (ges.):
Formel:
Rechnung:
Antwort:
Gegebene Werte:
Masse des Koffers (m) = 20 kg
Hubhöhe (h) = 2 m
Zeit (t) = 10 s
Erdbeschleunigung (g) ≈ 9,8 m/s²
Probiere es zunächst alleine. Wenn Du es nicht alleine schaffst, kannst Du hier noch eine Hilfe bekommen:
Zuerst berechnen wir die aufgebrachte Arbeit (W) mithilfe der Formel für die Hubarbeit: W = m * g * h.
Dann verwenden wir die Formel für die mechanische Leistung (P): P = W / t.
P = (m * g * h) / t
P = (20 kg * 9,8 m/s² * 2 m) / 10 s = 39,2 Watt
Antwort: Die mechanische Leistung beträgt 39,2 Watt.
Der Flaschenzug
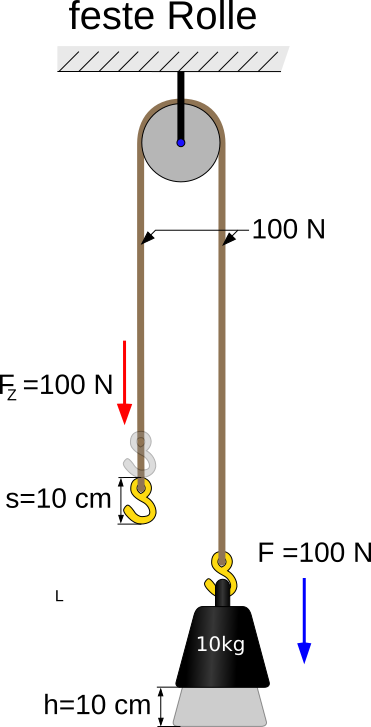
Stelle Dir ein Seil vor, das um eine fest an der Decke angebrachte Rolle führt. Rechts ist am Seil ein Gewicht angebracht. Links kannst Du am Seil ziehen.
Um das Gewicht hochzuziehen, musst Du die gleiche Kraft aufbringen, die die Gewichtskraft, die das Gewicht zur Erdmitte anzieht. Durch die feste Rolle wird die Kraft also einfach nur auf die andere Seite umgelenkt. Man spart keine Kraft ein.
Jetzt ändern wir den Versuchsaufbau: Das eine Ende des Seils befestigen wir an der Decke. Das Seil geht um eine Rolle, die frei nach unten hängt. An der Rolle hängt ein Gewicht:
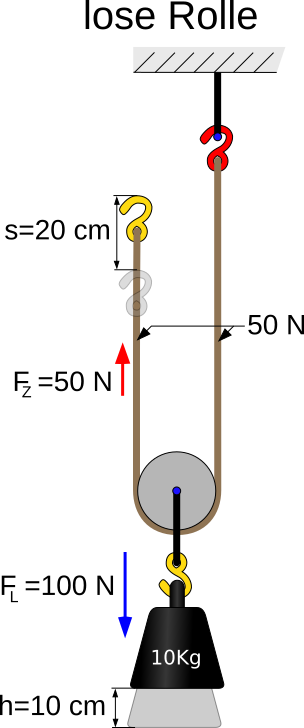
Jetzt passiert etwas Erstaunliches: Man stellt fest, dass man weniger Kraft braucht, um das Gewicht nach oben zu ziehen. Man braucht nur noch die Hälfte der Kraft, um das Gewicht 10 cm hochzuziehen. Allerdings muss ich das Seil nicht 10 cm hochziehen, sondern 20 cm. D.h. ich brauche zwar nur die Hälfte der Kraft, muss sie aber auf einer doppelten Strecke einsetzen.
Erinnern wir und an die Arbeit ( W=F*s ). Muss ich weniger Arbeit einsetzen, wenn ich eine lose Rolle einsetze? Nein! Da sich der Wert für die Strecke ( s ) verdoppelt, bleibt die Arbeit gleich. Allerdings brauche ich weniger Kraft.
Aufgabe: Schreibe einem Freund oder einer Freundin einen Brief über die wichtigsten Erkenntnisse zur festen und zur losen Rolle. Überschrift: Feste und lose Rolle.
Und jetzt noch eine Übung. Übertrage die fertigen Sätze in Deinen Hefter oder Dein Heft:
In der folgenden Animation wird Dir noch einmal Schritt für Schritt die feste und die lose Rolle erklärt:
Wau, daraus lässt sich doch etwas machen! Wie wäre es, wenn man noch mehr lose Rollen einbaut:
Der Hebel
Benutzt man einen Flaschenzug, so benötigt man weniger Kraft, die sich jedoch auf eine längere Strecke verteilt. Es gibt noch ein zweites einfaches Werkzeug, mit dem Du genau das Gleiche erreichen kannst. Und Du hast bestimmt schon einmal drauf gesessen: Die Wippe. Physiker sprechen dabei aber lieber von einem Hebel.

Ein Hebel ist eine starre Stange, die sich um einen Punkt dreht. Mit einem
Hebel können Kräfte übertragen werden. Im Allgemeinen benutzt man ihn da-
zu, um Kräfte zu verstärken. Man unterscheidet zwei Arten von Hebeln:
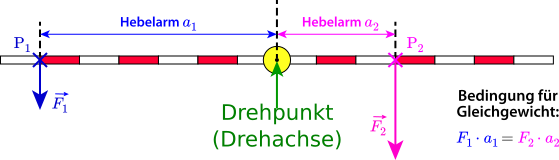
A. Zweiseitiger Hebel
Der Drehpunkt liegt zwischen Anfang und Ende der Hebelstange. Auf der
einen Seite des Drehpunktes, wo der Angriffspunkt der Kraft ist, liegt der He-
belarm (Kraftarm), während auf der anderen Seite, wo der Angriffspunkt der
Last ist, der Hebelarm (Lastarm) liegt.
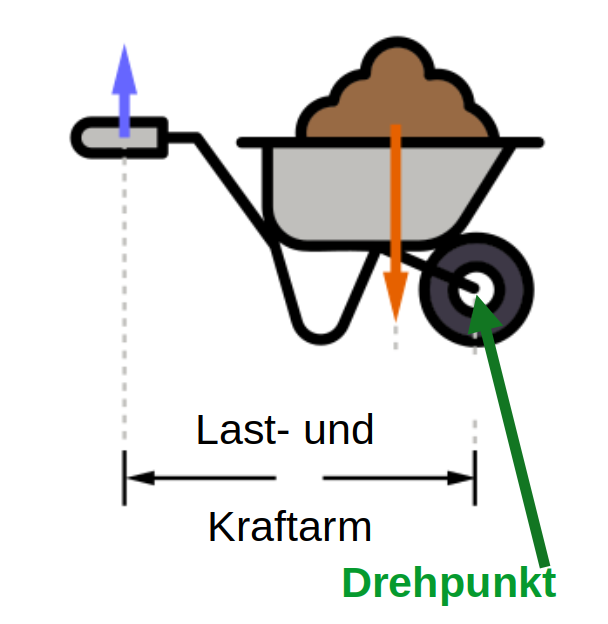
B. Einseitiger Hebel
Der Drehpunkt liegt am Ende der Hebelstange. Kraftarm und Lastarm befinden
sich auf derselben Seite.
[mwai_chatbot_v2]